W trzecim, a zarazem ostatnim, wpisie z cyklu związanego z moimi badaniami wpływu wstępnej filtracji obrazu na jego segmentację przedstawię wyniki jakie udało się mi zaobserwować i płynące z nich wnioski.

Badanie wpływu wstępnej filtracji obrazu na ilość segmentów po segmentacji

W części badawczej pracy postanowiono przeprowadzić analizę wpływu zastosowanych wstępnych filtrów na ilość segmentów na obrazie po segmentacji wododziałowej. Przebadano następujące filtry:

  • erozja, parametrem jest ilość iteracji
  • dylacja, parametrem jest ilość iteracji
  • otwarcie, parametrem jest ilość iteracji erozji i dylacji, oraz rozmiar elementu strukturalnego
  • zamknięcie, parametrem jest ilość iteracji erozji i dylacji, oraz rozmiar elementu strukturalnego
  • otwarcie i zamknięcie, parametrem jest ilość iteracji erozji i dylacji, oraz rozmiar elementu strukturalnego
  • filtr medianowy, parametrem jest rozmiar okna
  • filtr rozmyty, parametrem jest próg podobieństwa

Ponadto powtórzono badania dla obrazu po zastosowaniu wyrównania histogramu.

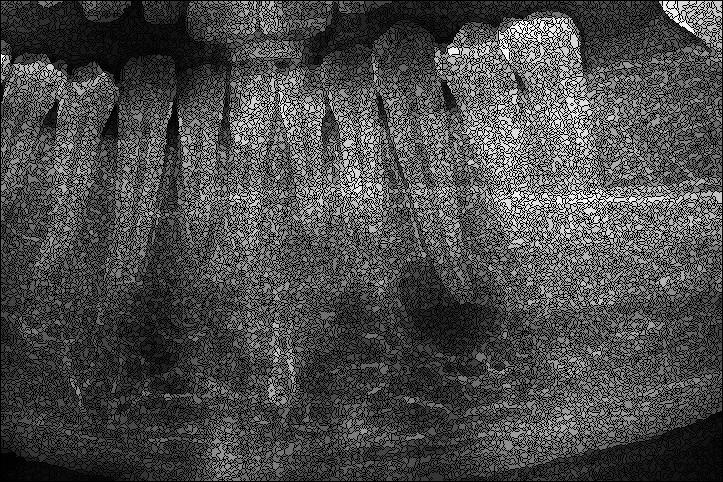
Badania przeprowadzono na obrazie RTG przedstawiającym dysplazję w postaci torbieli okołowierzchołkowej.

Badania rozpoczęto od wykonania segmentacji na obrazie nie poddawanym wcześniej żadnym filtracjom, rysunek 1. W tym przypadku na obrazie zliczono 30919 segmentów. Sprawdzono także wpływ samego wyrównania histogramu na ilość segmentów, w wyniku otrzymano obraz z 30196 segmentami.

Wynik segmentacji obrazu bez wstępnej filtracji
Rysunek 1: Wynik segmentacji obrazu bez wstępnej filtracji

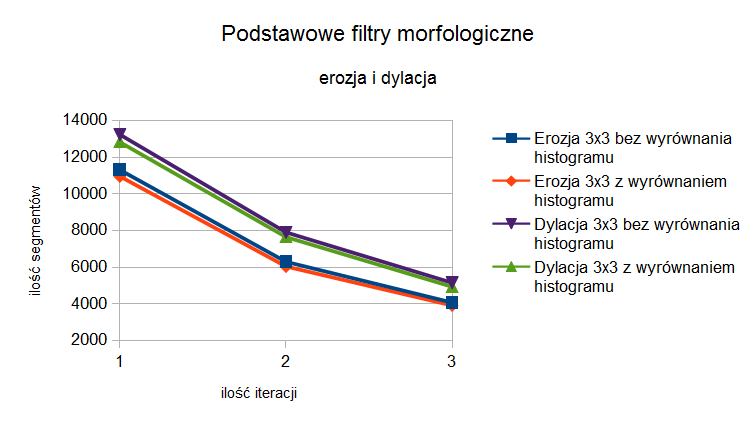
Podstawowe przekształcenia morfologiczne - erozja i dylacja

Badania postanowiono rozpocząć od sprawdzenia wpływu podstawowych filtrów morfologicznych - erozji i dylacji - na ilość segmentów w obrazie po segmentacji wododziałowej. Przyjęto kształt elementu strukturalnego jako kwadrat o boku równym 3, z punktem odniesienia ustawionym pośrodku. Jako parametr postanowiono przyjąć ilość wywołań filtru na obrazie wejściowym. Wyniki przedstawiono w tabelach 1, 2, 3, 4. Graficzną interpretację wyników pokazano na rysunku 2. Na wykresie można zauważyć, że zarówno w przypadku zastosowania erozji jak i dylacji, uzyskano ponad dwukrotne zmniejszenie ilości segmentów już przy pierwszej iteracji. Ilość segmentów spada wraz z kolejnymi iteracjami w podobnym tempie dla erozji i dylacji. Wyrównanie histogramu przynosi zawsze jedynie niewielki spadek ilości segmentów. Oba filtry, wraz z kolejnymi iteracjami powodują coraz większe zmiany w kształcie wyodrębnianych segmentów. Jest to zwłaszcza widoczne na granicy pomiędzy obserwowaną zmianą chorobową, której kolor jest ciemny, a korzeniem zęba przy którym zmiana się ta znajduje, który jest jasny. W przypadku dylacji jasne segmenty w obrębie korzenia poszerzają się nachodząc na obszar pierwotnie rozpoznawany jako lezja. Jest to spowodowane tym, że dylacja działa jak filtr maksymalny. W przypadku erozji obserwowany efekt jest odwrotny, segmenty mające reprezentować korzeń zostają zmniejszone, a w ich miejsce narastają segmenty reprezentujące lezje. Dzieje się tak ponieważ erozja działa jak filtr minimalny. Uzyskane wyniki badań wskazują, że w przypadku dylacji liczba segmentów jest mniejsza niż przy tej samej ilości iteracji dla erozji. Dzieje się tak, ponieważ w przypadku dylacji dochodzi do złączenia regionów o podobnych poziomach szarości, pomiędzy którymi występowały niewielkie regiony o odcieniach szarości mniejszych.

Tabela 1: Erozja - ilość segmentów w zależności od ilości iteracji, bez wyrównania histogramu
Ilość iteracji
1 2 3
Rozmiar elementu strukturalnego 3x3 11313 6294 4070
Tabela 2: Erozja - ilość segmentów w zależności od ilości iteracji, z wyrównaniem histogramu
Ilość iteracji
1 2 3
Rozmiar elementu strukturalnego 3x3 10957 6042 3911
Tabela 3: Dylacja - ilość segmentów w zależności od ilości iteracji, bez wyrównania histogramu
Ilość iteracji
1 2 3
Rozmiar elementu strukturalnego 3x3 13238 7900 5150
Tabela 4: Dylacja - ilość segmentów w zależności od ilości iteracji, z wyrównaniem histogramu
Ilość iteracji
1 2 3
Rozmiar elementu strukturalnego 3x3 12827 7644 4929
Podstawowe przekształcenia morfologiczne - erozja i dylacja - zależność ilości segmentów od ilości iteracji
Rysunek 2: Podstawowe przekształcenia morfologiczne - erozja i dylacja - zależność ilości segmentów od ilości iteracji

Złożone przekształcenia morfologiczne - otwarcie i zamknięcie

Kolejnym krokiem po przebadaniu podstawowych filtrów morfologicznych była analiza skutków połączenia tych filtrów w bardziej złożone algorytmy. Przeprowadzono badania dla otwarcia, zamknięcia oraz połączenia tych filtrów.

Tabela 5: Otwarcie - ilość segmentów w zależności od ilości iteracji i rozmiaru elementu strukturalnego, bez wyrównania histogramu
Ilość iteracji
1 2 3
Rozmiar elementu strukturalnego 3x3 14569 8616 5693
5x5 8616 4025 2380
Tabela 6: Otwarcie - ilość segmentów w zależności od ilości iteracji i rozmiaru elementu strukturalnego, z wyrównaniem histogramu
Ilość iteracji
1 2 3
Rozmiar elementu strukturalnego 3x3 14102 8310 5477
5x5 8300 3843 2222
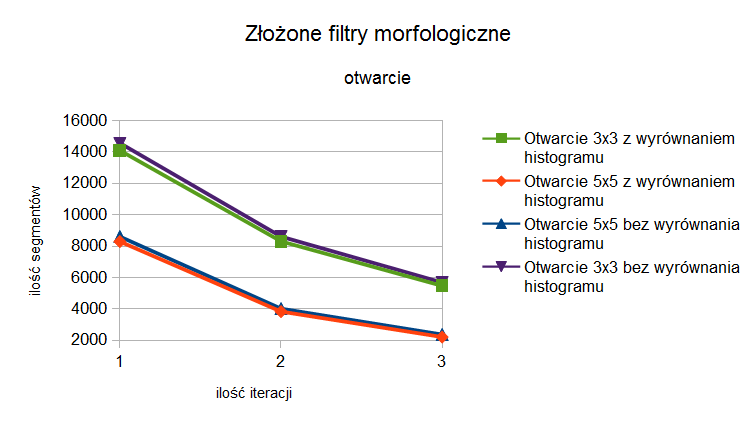
Złożone przekształcenia morfologiczne - otwarcie - zależność ilości segmentów od ilości iteracji
Rysunek 3: Złożone przekształcenia morfologiczne - otwarcie - zależność ilości segmentów od ilości iteracji

W tabelach 5 i 6 zawarto wartości ilości zliczonych segmentów po zastosowaniu operacji otwarcia morfologicznego. Na rysunku 3 pokazano te wyniki w postaci wykresu. Można zauważyć, że dla otwarcia z elementem strukturalnym o rozmiarze 3x3, wyniki są porównywalne do wyników otrzymanych dla podstawowych filtrów morfologicznych, gdzie zastosowano element strukturalny o tym samym rozmiarze. Po zmianie rozmiaru elementu strukturalnego na 5x5, zauważono dwukrotny spadek ilości segmentów na obrazie wyjściowym. W przypadku otwarcia problem zmiany kształtu segmentów granicznych pomiędzy lezją a jej otoczeniem, nie jest tak duży jak w przypadku podstawowych filtrów morfologicznych, zwłaszcza dla elementu strukturalnego 3x3 i pierwszej iteracji elementem 5x5. Spowodowane jest to tym, że operacja otwarcie jest złożeniem operacji erozji i dylacji. Operacja otwarcia powoduje usunięcie niewielkich ciemniejszych obszarów z otoczenia większych jasnych obszarów.

Tabela 7: Zamknięcie - ilość segmentów w zależności od ilości iteracji i rozmiaru elementu strukturalnego, bez wyrównania histogramu
Ilość iteracji
1 2 3
Rozmiar elementu strukturalnego 3x3 10463 5892 3846
5x5 5892 2698 1654
Tabela 8: Zamknięcie - ilość segmentów w zależności od ilości iteracji i rozmiaru elementu strukturalnego, z wyrównaniem histogramu
Ilość iteracji
1 2 3
Rozmiar elementu strukturalnego 3x3 10105 5687 3729
5x5 5715 2590 1578
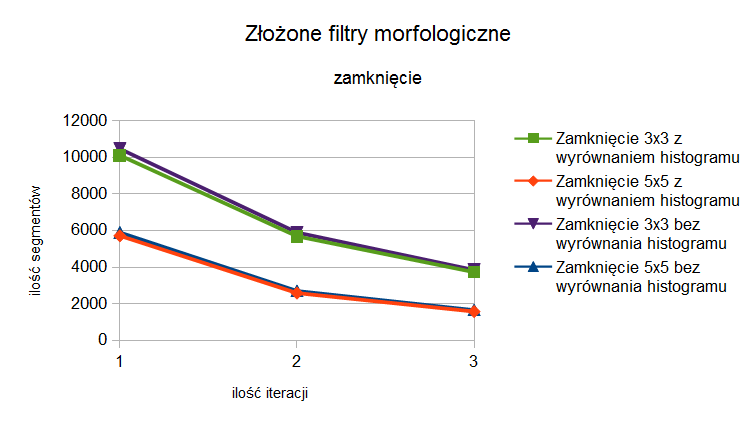
Złożone przekształcenia morfologiczne - zamknięcie - zależność ilości segmentów od ilości iteracji
Rysunek 4: Złożone przekształcenia morfologiczne - zamknięcie - zależność ilości segmentów od ilości iteracji

W tabelach 7 i 8 zawarto wartości ilości zliczonych segmentów po zastosowaniu operacji zamknięcia morfologicznego. Na rysunku 4 pokazano te wyniki w postaci wykresu. Można zauważyć, że ilość segmentów jest mniejsza od ilości otrzymanej w wyniku zastosowania otwarcia. Również w tym przypadku problem zmiany kształtu segmentów granicznych został ograniczony. Spowodowane to jest także tym, że operacja zamknięcia jest złożeniem erozji i dylacji, jednak w odwrotnej kolejności wykonywania tych operacji składowych. Segmentów jest mniej ponieważ najpierw wykonywana jest dylacja, która sama daje już mniejszą ilość segmentów niż erozja, a następnie na obrazie pośrednim wykonywana jest erozja.

Tabela 9: Otwarcie + zamknięcie - ilość segmentów w zależności od ilości iteracji i rozmiaru elementu strukturalnego, bez wyrównania histogramu
Ilość iteracji
1 2 3
Rozmiar elementu strukturalnego 3x3 6542 3179 1879
5x5 3179 1259 709
Tabela 10: Otwarcie + zamknięcie - ilość segmentów w zależności od ilości iteracji i rozmiaru elementu strukturalnego, z wyrównaniem histogramu
Ilość iteracji
1 2 3
Rozmiar elementu strukturalnego 3x3 6350 3070 1813
5x5 3070 1211 676
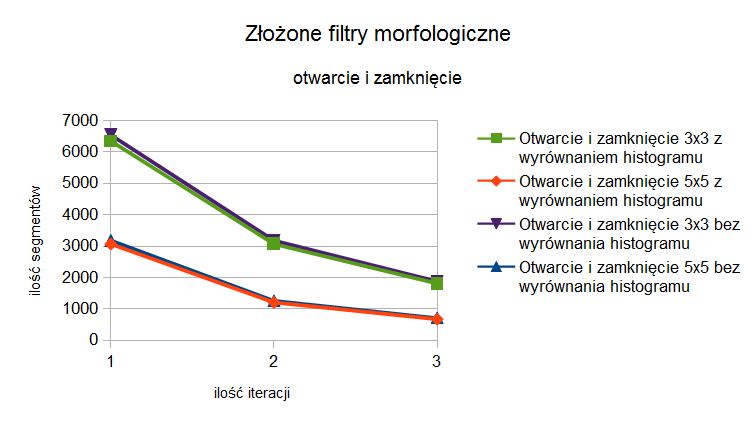
Złożone przekształcenia morfologiczne - otwarcie i zamknięcie - zależność ilości segmentów od ilości iteracji
Rysunek 5: Złożone przekształcenia morfologiczne - otwarcie i zamknięcie - zależność ilości segmentów od ilości iteracji

Postanowiono także przetestować działanie złożenia operacji otwarcia i zamknięcia. Wyniki testów umieszczono w tabelach 9 i 10, a ich wizualizację pokazano na rysunku 5. Uzyskano jeszcze większe ograniczenie ilości segmentów. Zastosowanie elementu strukturalnego 5x5 powoduje powstanie dużych segmentów i utratę informacji o kształcie torbieli. Podobne wyniki uzyskuje się dla elementu strukturalnego 3x3 przy dużej ilości iteracji. Jedynie po jednokrotnym zastosowaniu tego filtru otrzymane wyniki zachowują rozpoznawany kształt torbieli i korzenia.

Filtr medianowy

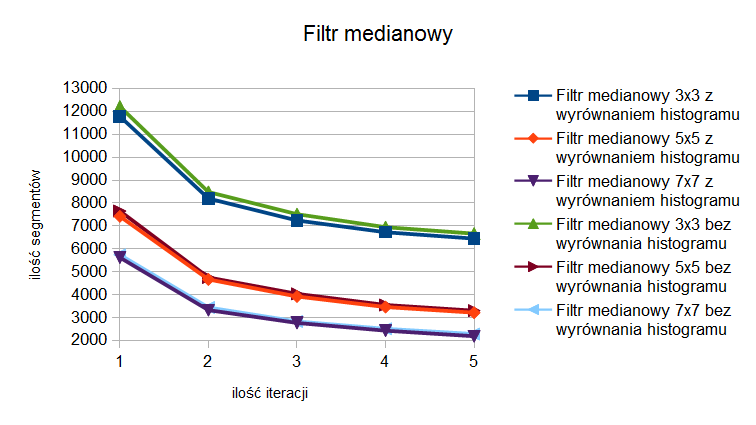
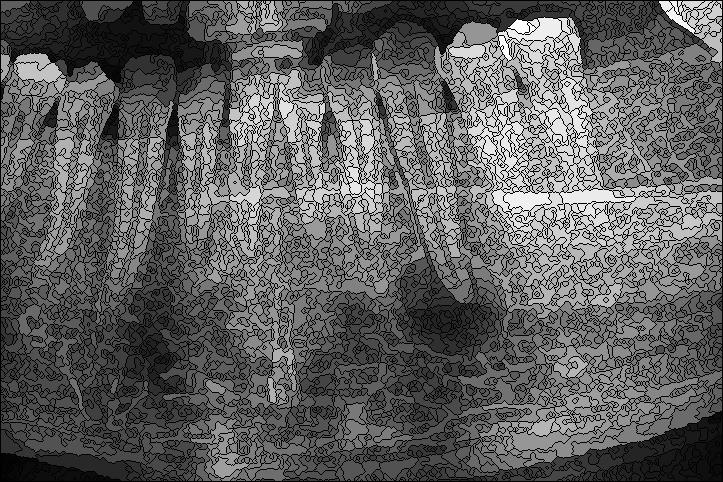
Ze zbioru uśredniających filtrów kontekstowych wybrano filtr medianowy. W tabelach 11 i 12 pokazano wyniki, a ich reprezentację graficzną umieszczono na rysunku 6. Można zauważyć, że otrzymane wielkości są porównywalne do wartości otrzymanych poprzednio dla złożonych filtrów morfologicznych. Wraz z zwiększaniem ilości iteracji, zachowując ten sam rozmiar okna otrzymuje się coraz mniej segmentów. Różnice te są jednak coraz mniejsze. Zwiększanie wielkości okna powoduje zmniejszenie ilości segmentów przy tej samej ilości iteracji. W tym przypadku także zwiększanie okna powoduje coraz mniejsze różnice w wynikach. W przypadku filtru medianowego problem zmiany kształtu segmentów granicznych nie jest widoczny nawet na obrazach poddanych wielu iteracjom, także tym gdzie rozmiar okna był większy. Granica pomiędzy torbielą, a korzeniem jest dobrze zaznaczona, wyostrzyła się. Na rysunku 7 pokazano wynik segmentacji obrazu po wstępnej filtracji filtrem medianowym o oknie 3x3, pięcioma iteracjami.

Tabela 11: Filtr medianowy - ilość segmentów w zależności od ilości iteracji i rozmiaru okna, bez wyrównania histogramu
Ilość iteracji
1 2 3 4 5
Rozmiar elementu strukturalnego 3x3 12215 8484 7515 6947 6664
5x5 7655 4752 4036 3551 3303
7x7 5740 3440 2830 2510 2283
Tabela 12: Filtr medianowy - ilość segmentów w zależności od ilości iteracji i rozmiaru okna, z wyrównaniem histogramu
Ilość iteracji
1 2 3 4 5
Rozmiar elementu strukturalnego 3x3 11784 8202 7241 6727 6449
5x5 7420 4665 3922 3462 3213
7x7 5621 3327 2766 2427 2187
Filtr medianowy - zależność ilości segmentów od ilości iteracji
Rysunek 6: Filtr medianowy - zależność ilości segmentów od ilości iteracji
Wynik segmentacji obrazu po wstępnej filtracji filtrem medianowym o oknie 3x3, pięcioma iteracjami
Rysunek 7: Wynik segmentacji obrazu po wstępnej filtracji filtrem medianowym o oknie 3x3, pięcioma iteracjami

Filtr rozmyty

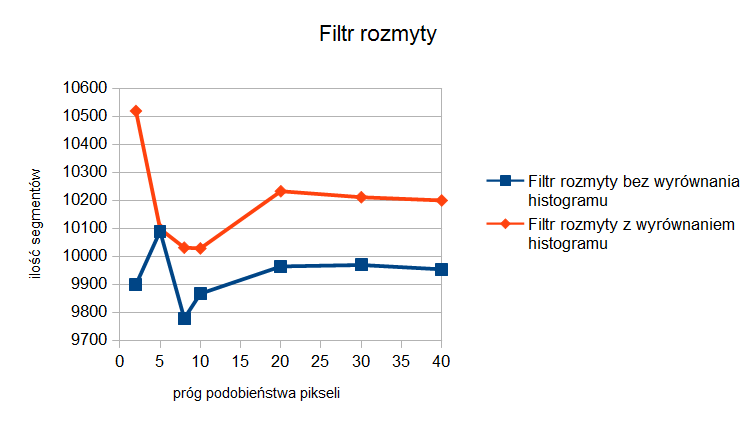
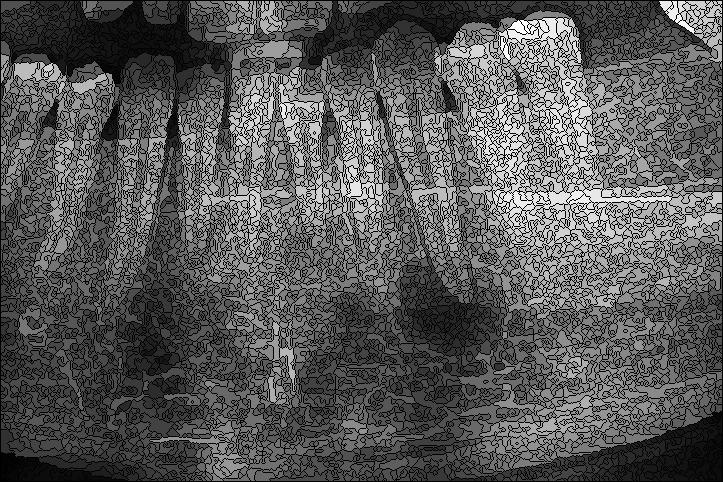
Ostatnim testowanym filtrem był filtr rozmyty zaimplementowany według opisu umieszczonego we wpisie wprowadzającym. Otrzymane wyniki pokazano w tabelach 13 i 14 oraz na rysunku 8. Parametrem dla którego badano wpływ jego zmian na ilość segmentów był próg podobieństwa, czyli wartość różnicy pomiędzy wartościami dwóch sąsiadujących pikseli po przekroczeniu której para ta była uznawana za niepodobną. Ponieważ wynik działania filtru ma charakter losowy, dla każdej wartości progu podobieństwa przeprowadzono pięć prób, po czym obliczono średnie wartości oraz rozrzut wokół wartości średniej. Okazało się, że filtr charakteryzuje się dużą stabilnością otrzymywanych wyników. Z otrzymanego wykresu wynika, że najmniej segmentów otrzymuje się dla wartości progu podobieństwa mieszczących się pomiędzy 5 a 10. Dla wartości mniejszych ilość segmentów jest największa, a dla wartości większych rośnie i stabilizuje się. Otrzymane minimalne wartości są trzy razy mniejsze niż w przypadku braku filtracji. Podobnie jak w przypadku filtru medianowego, nie występuje problem zmiany kształtu granic oddzielających torbiel od otoczenia. Na rysunku 9 pokazano wynik segmentacji obrazu po wstępnej filtracji filtrem rozmytym z progiem podobieństwa 8px.

Tabela 13: Filtr rozmyty - ilość segmentów w zależności od progu podobieństwa i próby, bez wyrównania histogramu
Próg podobieństwa
2 5 8 10 20 30 40
Próba 1 9894 10089 9747 9865 9974 9944 9967
2 9858 10101 9782 9893 9939 9967 9945
3 9881 10137 9784 9886 9956 9976 9955
4 9880 10071 9808 9860 10001 9973 9943
5 9983 10051 9772 9830 9951 9986 9959
Średnia 9899,2 10089,8 9778,6 9866,8 9964,2 9969,2 9953,8
Odchylenie standardowe 48,60 32,45 22,06 24,79 24,12 15,67 9,96
Tabela 14: Filtr rozmyty - ilość segmentów w zależności od progu podobieństwa i próby, z wyrównaniem histogramu
Próg podobieństwa
2 5 8 10 20 30 40
Próba 1 10457 10072 10060 10067 10294 10199 10238
2 10527 10103 10043 10046 10229 10216 10192
3 10595 10107 10016 10000 10165 10212 10187
4 10503 10091 10024 10028 10231 10213 10187
5 10518 10120 10013 10002 10246 10218 10197
Średnia 10520,0 10098,6 10031,2 10028,6 10233,0 10211,6 10200,2
Odchylenie standardowe 49,84 18,12 19,89 28,74 46,19 7,44 21,53
Filtr rozmyty - zależność ilości segmentów od ilości iteracji
Rysunek 8: Filtr rozmyty - zależność ilości segmentów od ilości iteracji
Wynik segmentacji obrazu po filtracji filtrem rozmytym z progiem podobieństwa 8px
Rysunek 9: Wynik segmentacji obrazu po filtracji filtrem rozmytym z progiem podobieństwa 8px

Badanie wpływu wstępnej filtracji obrazu na czas wykonania procesu segmentacji

Postanowiono zbadać czas wykonania procesu dla dwóch wybranych najlepszymi filtrów

  • filtru medianowego z oknem 3x3 i pięcioma iteracjami oraz dla filtru rozmytego z progiem podobieństwa ustawionym na 10 pikseli. Oba filtry zostały poprzedzone wyrównaniem histogramu. Postanowiono przeprowadzić po pięć prób dla każdego z filtrów. Badania przeprowadzono na tym samym obrazie testowym który zastosowano w poprzednich badaniach. Badania przeprowadzono na komputerze wyposażonym w procesor Athlon II X2 250 i 4GB pamięci RAM.

Filtr medianowy - czas wykonania procesu

W tabeli 15 umieszczono czasy wykonani poszczególnych operacji składających się na proces segmentacji, tj.: wstępnej filtracji, segmentacji oraz oznaczania segmentów. Operację oznaczania segmentów sprawdzono dla dwóch zaproponowanych algorytmów, SegmentMarkerBasic - powolnego algorytmu polegającego na złączaniu segmentów, SegmentMarkerFlooding - szybkiego algorytmu polegającego na sprawdzaniu pikseli sąsiadujących w pierwszej kolejności, algorytmy te zostaną opisane w kolejnych wpisach. W tabeli tej podano także całkowity czas wykonania procesu. W wyniku, dla obrazu testowego, otrzymano średni całkowity czas równy 182,33 sekund w przypadku zastosowania algorytmu SegmentMarkerBasic oraz 1,32 sekundy w przypadku zastosowania algorytmu SegmentMarkerFlooding. Operacja wykonania filtru medianowego na obrazie miała najmniejszy wpłyn na czas całkowity, podobnie operacja segmentacji wododziałowej. Operacja oznaczania segmentów, w przypadku wybrania wolniejszego algorytmu ma największy wpływ na całkowity czas procesu.

Tabela 15: Filtr medianowy - czas wykonania procesu segmentacji
Czas [s]
filtracja segmentacja oznaczanie segmentów (basic) oznaczanie segmentów (flooding) razem (basic) razem (flooding)
Próba 1 0,00 1,00 172,88 0,32 173,88 1,32
2 0,00 1,00 166,60 0,39 167,60 1,39
3 0,00 1,00 198,29 0,44 199,29 1,44
4 0,00 2,00 199,82 0,42 201,82 2,42
5 0,00 1,00 168,05 0,30 169,05 1,30
Średnia 0,00 1,20 181,13 0,37 182,33 1,57
Odchylenie standardowe 0,00 0,45 16,54 0,06 16,82 0,48

Filtr rozmyty - czas wykonania procesu

W tabeli 16 umieszczono zmierzone czasy poszczególnych składowych procesu w przypadku zastosowania filtru rozmytego. Składowe procesu są takie same jak w przypadku filtru medianowego. Wyniki wskazują na wzrost znaczenia czasy potrzebnego na filtrację obrazu w całym procesie. Średnio ten czas wynosi 24,40 sekund, co jest zauważalnym czasem, zwłaszcza przy zastosowaniu szybkiego algorytmu oznaczania segmentów. Jest to także duży wzrost w porównaniu do filtracji medianowej która wykonywana była niemal natychmiastowo. Średni czas całego procesu, w przypadku zastosowania algorytmu SegmentMarkerBasic wzrósł do 212,38 sekund, a w przypadku algorytmu SegmentMarkerFlooding czas ten wzrósł do 25,98 sekund.

Tabela 16: Filtr rozmyty - czas wykonania procesu segmentacji
Czas [s]
filtracja segmentacja oznaczanie segmentów (basic) oznaczanie segmentów (flooding) razem (basic) razem (flooding)
Próba 1 28,00 1,00 188,42 0,47 217,42 29,47
2 22,00 1,00 180,15 0,37 203,15 23,37
3 23,00 1,00 197,79 0,37 221,79 24,37
4 23,00 1,00 168,58 0,37 192,58 24,37
5 26,00 2,00 198,98 0,34 226,98 28,34
Średnia 24,40 1,20 186,78 0,38 212,38 25,98
Odchylenie standardowe 2,51 0,45 12,73 0,05 14,18 2,73

Wnioski

Przeprowadzono badania mające na celu wskazanie najlepszego, biorąc pod uwagę ilość i jakość otrzymanych segmentów, algorytmu przygotowującego zdjęcie do analizy. Wzięto pod uwagę podstawowe filtry morfologiczne, tj.: erozję i dylację, złożone filtry morfologiczne, tj.: otwarcie i zamknięcie oraz ich złożenie, filtr medianowy oraz filtr wykorzystujący logikę rozmytą. W wyniku przeprowadzonych badań, okazało się że filtry morfologiczne z powodu zmiany kształtu otrzymywanych w następstwie ich użycia segmentów granicznych, czyli znajdujących się w miejscach o największych zmianach gradientu, nie powinny być wykorzystywane do wstępnej filtracji obrazu przed jego segmentacją. Otrzymano dobre wyniki dla filtru medianowego o oknie 3x3, dla każdej ze zbadanych ilości iteracji. Filtr ten nie powoduje także zmiany kształtu segmentów granicznych. Dobre wyniki przyniosło także zastosowanie zaimplementowanego algorytmu wykorzystującego logikę rozmytą. Przeprowadzono badania polegające na znalezieniu optymalnej wartości progu podobieństwa, jednego z parametrów tego algorytmu, dla której ilość segmentów jest najmniejsza. Wyznaczono lokalne minimum dla tego parametru, wynoszące 10 pikseli. Oznacza to że dla mniejszej i większej wartości progu filtr ten działa gorzej nie odnajdując wszystkich zaszumionych pikseli co powoduje wzrost lokalnych minimów obrazu a co za tym idzie ilości segmentów.

Przeprowadzono także badania polegające na zmierzeniu czasu jaki potrzebny jest na przeprowadzenie całego procesu segmentacji dla dwóch filtrów: filtru rozmytego z progiem 10px oraz filtru medianowego z oknem 3x3 i pięcioma iteracjami. Otrzymane wyniki wskazują, że filtr medianowy jest znacznie szybszy od zaimplementowanego filtru rozmytego. Jest to spowodowane większą złożonością obliczeniową algorytmu rozmytego, a także tym że filtr medianowy pochodził z napisanej w C++ i zoptymalizowanej do tego celu biblioteki OpenCV.

Po przeprowadzeniu badań zdecydowano się zaimplementować w systemie obsługującym gabinet dentystyczny algorytm wykorzystujący filtr medianowy z oknem 3x3 i pięcioma iteracjami.

Podczas testów czasu wykonania procesu segmentacji pokazano że największe narzut generuje algorytm SegmentMarkerBasic. Z powodu mogącego się pojawić wyjątku generowanego przez alternatywny algorytm został on jednak wybrany i zaimplementowany w systemie obsługi gabinetu dentystycznego.

Zamierzano napisać algorytm pozwalający na zautomatyzowanie procesu oznaczania na zdjęciach RTG patologicznych zmian okołowierzchołkowych zęba spowodowanych stanem zapalnym. Napisano algorytm wykorzystujący oznaczone segmenty, ograniczający ingerencję użytkownika do wybrania segmentu znajdującego się wewnątrz takiej zmiany oraz drugiego poza nią. Algorytm ten wybiera kolejne segmenty biorąc pod uwagę średnie wartości pikseli we wskazanych segmentach. Nie zawsze jednak wynik jego działania jest zgodny z oczekiwaniami. W związku z tym należałoby go rozbudować o algorytm działający w sposób adaptacyjny.

Treść tego wpisu zawiera fragmenty mojej pracy dyplomowej “Badanie wpływu wstępnej filtracji na proces segmentacji w analizie patologicznych zmian w obrębie zębów widocznych na zdjęciach RTG”.

Zobacz także: